a) En utilisant exclusivement l�alg�bre bool�ene, d�montrez que :
b) En utilisant la d�composition de Shannon, d�montrez que :
c) En utilisant une technique de votre choix, d�montrez que le circuit suivant a toujours sa sortie fausse :
Exercice 2 � Analyse et synth�se de circuits
1) La fonction FX est sp�cifi�e par sa table de v�rit� :
Trouver l�expression disjonctive simplifi�e de X au moyen de la table de Karnaugh.
�valuez son co�t minimal et dessinez votre meilleur circuit
2) La fonction FY a d�j� �t� r�alis�e par un apprenti. Elle fonctionne bien mais le patron pr�tend que le circuit co�te trop cher pour rien. Faites l�analyse de cette fonction et proposez votre meilleur circuit en comparant les versions disjonctive et conjonctive.
c) Votre patron vous demande de porter un regard critique sur la premi�re implantation de FY. Qu�allez-vous lui dire ?
3) Sachant que finalement, seule la valeur de Z importe, proposez votre meilleur circuit pour implanter Z(A,B,C,D)
Exercice 3 - Quine-McCluskey
1) Retranscrire les minterms de la fonction F sous forme binaire en soulignant les minterms facultatifs � exemple : 0110 pour
2) Proc�der par la m�thode Quine-McCluskey pour simplifier la fonction F(A,B,C,D) et identifier les impliquants premiers
3) Utiliser la table suivante pour identifier les impliquants essentiels de F(A,B,C,D)
4) Utilisez la m�thode de Petrick simplifi�e (apr�s �limination des impliquants essentiels) pour trouver toutes les solutions (les moins ch�res) possibles. �crivez chaque solution sous sa forme alg�brique (disjonctive).
5) Confirmez votre r�sultat en utilisant une table de Karnaugh
Exercice 4 - D�codeur

De m�me,
Apr�s distribution et commutation, on obtient les deux m�mes expressions.
b) Par Shannon, sur la variable A, il vient :
Par Shannon sur la variable B, il vient :
c) En utilisant une technique de votre choix, d�montrez que le circuit suivant a toujours sa sortie fausse :
Soit X, la sortie du XNOR(B,C), il vient, par Shannon sur la variable X :
Exercice 2 � Analyse et synth�se de circuits
1) Trouver l�expression disjonctive simplifi�e de X au moyen de la table de Karnaugh.
�valuez son co�t minimal et dessinez votre meilleur circuit
Dessinez le circuit ci-dessous
a) version disjonctive
b) version conjonctive
C��tait une bonne id�e d�utiliser la forme conjonctive. Toutefois, deux erreurs ont �t� commises :
1) 3 impliqu�s alors que 2 auraient suffi
2) L�utilisation de portes NOR aurait �t� moins couteuse
Conclusion, le patron avait raison, le circuit coute (2+2)+(3+2)+(3+2)+(3+2), soit 19 � la place de 9.
Dessinez le circuit optimis�.
Exercice 3 - Quine-McCluskey
1)

b) En utilisant la d�composition de Shannon, d�montrez que :
c) En utilisant une technique de votre choix, d�montrez que le circuit suivant a toujours sa sortie fausse :
Exercice 2 � Analyse et synth�se de circuits
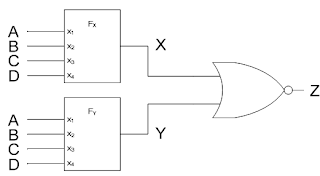
L�implantation d�une fonction logique Z relativement complexe repose sur un NOR de deux autres fonctions FX et FY comme indiqu� sur le sch�ma suivant :
1) La fonction FX est sp�cifi�e par sa table de v�rit� :
Trouver l�expression disjonctive simplifi�e de X au moyen de la table de Karnaugh.
�valuez son co�t minimal et dessinez votre meilleur circuit
2) La fonction FY a d�j� �t� r�alis�e par un apprenti. Elle fonctionne bien mais le patron pr�tend que le circuit co�te trop cher pour rien. Faites l�analyse de cette fonction et proposez votre meilleur circuit en comparant les versions disjonctive et conjonctive.
c) Votre patron vous demande de porter un regard critique sur la premi�re implantation de FY. Qu�allez-vous lui dire ?
3) Sachant que finalement, seule la valeur de Z importe, proposez votre meilleur circuit pour implanter Z(A,B,C,D)
Exercice 3 - Quine-McCluskey
Soit la table de v�rit� de la fonction logique F(A,B,C,D) :
1) Retranscrire les minterms de la fonction F sous forme binaire en soulignant les minterms facultatifs � exemple : 0110 pour

2) Proc�der par la m�thode Quine-McCluskey pour simplifier la fonction F(A,B,C,D) et identifier les impliquants premiers
3) Utiliser la table suivante pour identifier les impliquants essentiels de F(A,B,C,D)
4) Utilisez la m�thode de Petrick simplifi�e (apr�s �limination des impliquants essentiels) pour trouver toutes les solutions (les moins ch�res) possibles. �crivez chaque solution sous sa forme alg�brique (disjonctive).
5) Confirmez votre r�sultat en utilisant une table de Karnaugh
Exercice 4 - D�codeur
En utilisant un d�codeur (3 bits de s�lection A, B et C) et une seule porte logique � deux entr�es par fonction, implantez les fonctions F1, F2, F3 et F4
Exercice 5 - multiplexeur
Exercice 5 - multiplexeur
En utilisant un multiplexeur (4 vers 1, 2 bits de s�lection) et une seule porte logique, implantez la fonction suivante :
Suggestion : utilisez la r�duction sur les variables C et D
Correction
Exercice 1 � Alg�bre de Boole
a) En utilisant exclusivement l�alg�bre bool�ene, d�montrez que :
On calcule les formes canoniques disjonctives des deux expressions :
De m�me,
Apr�s distribution et commutation, on obtient les deux m�mes expressions.
b) Par Shannon, sur la variable A, il vient :
Par Shannon sur la variable B, il vient :
c) En utilisant une technique de votre choix, d�montrez que le circuit suivant a toujours sa sortie fausse :
Soit X, la sortie du XNOR(B,C), il vient, par Shannon sur la variable X :
Exercice 2 � Analyse et synth�se de circuits
1) Trouver l�expression disjonctive simplifi�e de X au moyen de la table de Karnaugh.
�valuez son co�t minimal et dessinez votre meilleur circuit
Dessinez le circuit ci-dessous
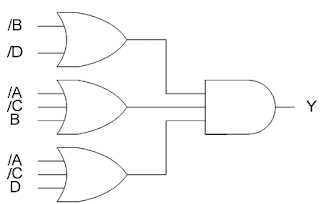
2) La fonction FY a d�j� �t� r�alis�e par un apprenti. Elle fonctionne bien mais le patron pr�tend que le circuit co�te trop cher pour rien. Faites l�analyse de cette fonction et proposez votre meilleur circuit en comparant les versions disjonctive et conjonctive.
a) version disjonctive
b) version conjonctive
c) Votre patron vous demande de porter un regard critique sur la premi�re implantation de FY. Qu�allez-vous lui dire ?
C��tait une bonne id�e d�utiliser la forme conjonctive. Toutefois, deux erreurs ont �t� commises :
1) 3 impliqu�s alors que 2 auraient suffi
2) L�utilisation de portes NOR aurait �t� moins couteuse
Conclusion, le patron avait raison, le circuit coute (2+2)+(3+2)+(3+2)+(3+2), soit 19 � la place de 9.
3) Sachant que finalement, seule la valeur de Z importe, proposez votre meilleur circuit pour implanter Z(A,B,C,D)
Dessinez le circuit optimis�.
Exercice 3 - Quine-McCluskey
1)
2) Proc�der par la m�thode Quine-McCluskey pour simplifier la fonction F(A,B,C,D) et identifier les impliquants premiers
3) Impliquants essentiels : 0X1X
4)

Soient 4 solutions optimales avec 3 impliquants premiers (+ l�impliquant essentiel)
5) Confirmez votre r�sultat en utilisant une table de Karnaugh
Exercice 4 - D�codeur
Exercice 5 - multiplexeur